
封图来源:Unsplash
撰文 | 杰克·默塔(Jack Murtagh)
翻译 | 陶兆巍
当你在线上购物,选好商品下单后,你来到了支付页面,准备输入银行卡号。还没敲回车,屏幕上就跳出红色警告:“请输入有效的银行卡号。”你恼火地逐位检查,终于发现问题:本该是5的位置打成了6。修正后,支付顺利完成。但网站是如何快速发现错误的?难道他们存储了所有有效卡号?这个问题的答案其实很巧妙。
所有银行卡号都采用了一种专门用于捕捉常见输入错误的数学技巧。这种技巧被称为卢恩算法(Luhn algorithm),以美国IBM公司研究员汉斯·彼得·卢恩(Hans Peter Luhn)的名字命名,他在1960年为该算法申请了专利。类似的错误检验机制潜藏在你日常接触的许多数字中,比如,条形码、银行账号,甚至书籍的ISBN号等。
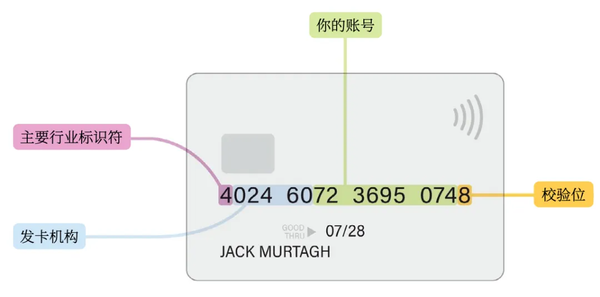
拿出一张银行卡,你会发现卡号的结构远比表面上看起来复杂。一个银行卡卡号的构成包括四个主要部分。以我个人的Visa卡为例:
第一位数字是主要行业标识符。Visa卡总是以4开头,而Discover卡以6开头。接下来的五到七位数字确定了发卡银行或机构。剩余部分(除去末位)是你在该银行的具体账号。最后一位,有时被称为校验位(check digit),与金融机构无关。发卡方添加它,是为了让整个卡号能够通过一个特定的数学检验——卢恩算法。该算法的工作流程如下:
1.写下卡号除最后一位外的所有数字。
2.从右往左,每隔一位将数字翻倍。
3.将所有得到的数位(注意不是数字本身)相加。例如,你在第2步将7翻倍成14,那么在这一步它会变成1+4=5。
4.将总和加上校验位。若末位不是0,则卡号无效。
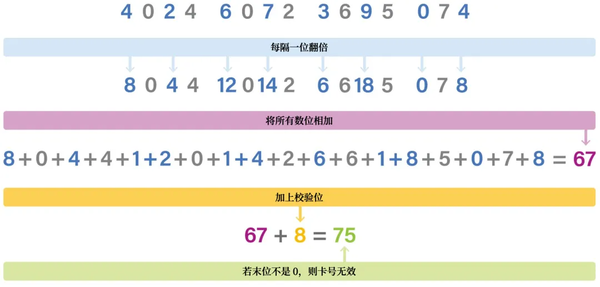
下面用我的Visa卡演示卢恩算法(你也可以用自己的银行卡试试)。结果是75,不是10的倍数。所以这不可能是我的真实卡号,我肯定打错了。
对于银行卡发卡方,他们会首先分配账号,然后执行卢恩算法的前三步来确定校验位。比如,我展示卡号的校验位应为3。这套算法之所以能主导银行卡验证,源于其简洁性和强大的功能。如果你在输入卡号时弄错了任何一位数字,卢恩算法都能检测出来。如果你不小心把相邻的两位数字顺序弄反了,它也能检测到(唯一的例外是09和90互换)。
那么,卢恩算法为什么能检测到单个数字的输入错误?如果错误发生在不翻倍的位置,则会改变这个求和项中的一个数字;如果发生在翻倍的位置,由于翻倍后再将两位数字求和的操作分别将(0,1,2,…,9)变成了(0,2,4,6,8,1,3,5,7,9),错误仍然会改变求和项中的一个数字。因此任何单个数字输入错误肯定会导致总和不是10的倍数。
形式化地证明卢恩算法能检测相邻数字互换需要一些分类讨论,但以下例子可以说明其原理。假设我们的银行卡号中有序列31,其中3处于翻倍位置。我们不小心输成了13。在正确的总和中,这对数字贡献(3×2)+1=7,而在错误的总和中,它贡献(1×2)+3=5。因此这个错误最终使我们的总和改变了2,从而破坏了总和除以10的余数。我们只需验证这对所有数字对(除了09和90)都成立即可。
荷兰数学家雅各布斯·费尔霍夫(Jacobus Verhoeff)在1969年报告称,这两类错误——单个数字输错和相邻数互换——在实际应用中占人工输入错误的近90%。费尔霍夫开发了一种更全面的算法,除了能检测卢恩算法能检测的所有错误外,还能捕捉09和90的互换,以及更多罕见的失误。费尔霍夫算法堪称一项数学成就。当时甚至有人发表过错误的证明,声称单个校验位不可能携带足够的信息来捕捉所有这些错误。然而,费尔霍夫算法从未被广泛采用,也许是因为它更复杂,也可能是因为卢恩算法已经广泛应用,且效果足够好。
卢恩算法不仅能节省你的时间,也能节省商家的成本。如果没有这种数学技巧,每次网购付款,商家都需要将你的信息发送到专门的银行卡验证服务机构,来确认卡片属于你本人。这种通信既浪费时间,也耗费金钱。而卢恩算法所需的算力极小,本地计算机即可自行检查这类常见输入错误,无需任何昂贵的通信手段。
需要注意的是,通过卢恩算法检验并不能保证卡号有效,但未通过检验则代表卡号一定无效。该算法构建了第一道防线,一些不常见的输入错误和诈骗者仍有可能绕过它。而这些情况会被更消耗资源的银行卡验证服务捕获。
下次当你在银行卡支付页面再遇到那条恼人的错误提示时,请记住:底层的一段简单数学代码为所有人都节省了一点时间或金钱。
本文来自《环球科学》2025年12月刊《银行卡号的数学秘密》一文。
